题目链接：

题意：

思路：不妨设a=1,b=2,

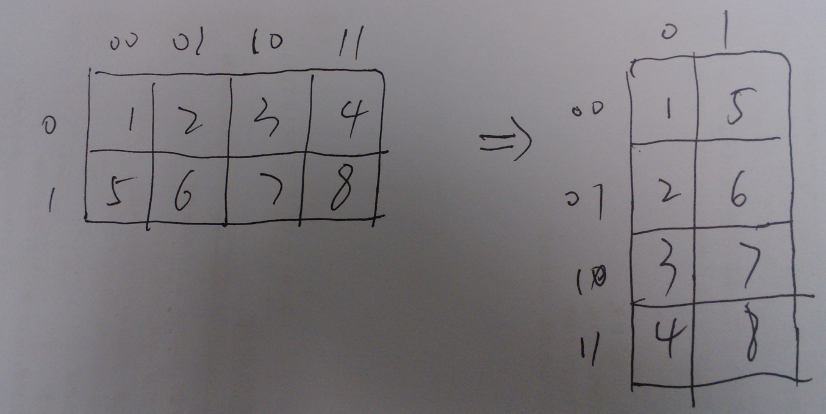
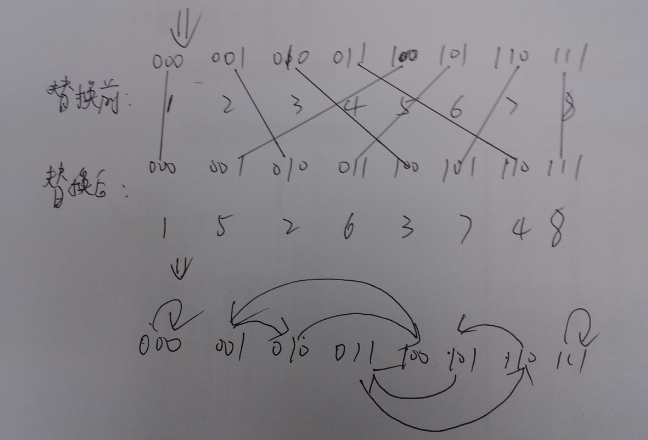
我们发现(001,010,100)组成一个置换，(011,110,101)组成一个置换。那么对于同一个置换中元素，设置换大小为x，则需要x-1次交换。因此，我们若找到循环节的个数K，那么答案即为2^(a+b)-K.

a+b个珠子的项链，每个珠子可以用两种颜色涂色，通过每次左移a个珠子得到的相同的视为相同。求不同项链的个数。问题就转化成这个。设g=Gcd(a,a+b)，则置换群个数为G=(a+b)/g。其实可以看做有G个珠子，每个珠子可以用2^g种颜色涂色。答案为：

 

int a,b,Pow[N],phi[N];int prime[1005],tag[1005],cnt;void init(){    Pow[0]=1;    int i,j;    for(i=1;i
     
      1) p[num]=n,q[num++]=1;}int ans,m,L;int calPow(int a,int b){    int ans=1;    while(b)    {        if(b&1) ans=(i64)ans*a%mod;        a=(i64)a*a%mod;        b>>=1;    }    return ans;}void cal(int t){    int x=L/t;    ans+=(i64)calPow(m,t)*phi[x]%mod;    ans%=mod;}void DFS(int dep,int t){    if(dep==num)    {        cal(t);        return;    }    int i;    for(i=0;i<=q[dep];i++)    {        DFS(dep+1,t);        t*=p[dep];    }}int main(){    init();    rush()    {        RD(a,b);        if(!a||!b)        {            puts("0");            continue;        }        b+=a;        int k=Gcd(a,b);        L=b/k;        split(L); ans=0; m=Pow[k];        DFS(0,1);        i64 x,y;        exGcd(L,mod,x,y);        x=(x%mod+mod)%mod;        ans=ans*x%mod;        ans=Pow[b]-ans;        ans=(ans%mod+mod)%mod;        PR(ans);    }}